Going deep into backpropagation

[[toc]]

• Backpropagation
  • Some references
  • Algorithm
    • Definitionsss
    • Steps
      • Assumptions about Dimensions
      • Algorithm
  • Elaboration about Derivatives
    • 3. Step - Calculating $\frac{\partial E}{\partial z^{l}} = \delta^{l}$
      • Calculating $\frac{\partial E}{\partial z^{L}} = \delta^{L}$
      • Calculating $\frac{\partial E}{\partial z^{L-1}}=\delta^{(L-1)}, \frac{\partial E}{\partial z^{L-2}}=\delta^{(L-2)},\dots, \frac{\partial E}{\partial z^{2}}=\delta^{(2)}$ GENERAL CASE
    • 4. Step - Calculating $\frac{\partial E}{\partial \theta^{l}}$
  • Gradient Checking

Backpropagation

I have written this description about the intrinsics of backpropagation to get a quick and clear insight into the idea and the mathematics of backpropagation in a level which a first year CS master student should understand. I myself use this for a quick reminder, so maybe the best purpose for this should be recap. At least the mathematics should be generally correct

Some references

• https://www.coursera.org/learn/machine-learning/supplement/pjdBA/backpropagation-algorithm
• https://mattmazur.com/2015/03/17/a-step-by-step-backpropagation-example/

Why it is important to know this

• https://medium.com/@karpathy/yes-you-should-understand-backprop-e2f06eab496b

Algorithm

Definitionsss

• K = number of output units
• L = number of layers in network
• $s_{l} =$ number of units in layer l
• m = number of training examples
• E - another symbol for cost function J
• $\lambda$ - regularization term
• $$\theta^{L}_{ij}$$
• $\Delta$ - this is used for cumuating the gradietns calculated on every training example for every theta
• D - final gradient after one iteration of backpropagation.

Steps

Assumptions about Dimensions

• We currently do backpropagation on every training example separately

FORWARD PROPAGATION DIMENSION SPECIFICATION

If network has $s_{j}$ units in layer j and $s_{j+1}$ units in layer j+1, then $\theta^{j}$ will have $s_{j+1}$ rows and $s_{j}+1$ columns. (The +1 for $\theta$ columns comes from bias nodes).

This result in $a^{j+1}$ (and also $z^{j+1}$ ) being a vector with dimensions $s_{j+1}$ X $1$

BACKPROPAGATION DIMENSIONS SPECIFICATION

Continuing with the last example, $\delta^{j+1}$ has also $s_{j+1}$ X $1$ dimensions. Hint to backpropagation part later on: $(\theta^{j})^{T}\delta^{j+1}$

Algorithm

Initialize $\Delta^{l}_{ij}=0, \forall ij\text{ and }l$

REPEAT FOR $1\dots m$

1. Perform Forward Propagation. This can be done using the training matrix as well. Result is going be in the size of (m * K ).

Example of forward propagation

1. Calculate the cost
   • Definitions
     • $\theta$ - Hypothesis function parameters
     • $h_{\theta}()_ {k}$ Hypothesis function
     • $x^{(i)}$ i-th training data
   • $$J(\Theta) = - \frac{1}{m} \sum_{i=1}^m \sum_{k=1}^K \left[y^{(i)}_k \log ((h_\Theta (x^{(i)}))_ k) + (1 - y^{(i)}_k)\log (1 - (h_\Theta(x^{(i)}))_ k)\right] + \frac{\lambda}{2m}\sum_ {l=1}^{L-1} \sum_{i=1}^{s_l} \sum_{j=1}^{s_{l+1}} ( \Theta_{j,i}^{(l)})^2$$
2. Calculate derivatives of Cost Function according to every $z^{l}_{s}$ $\frac{\partial E}{\partial z^{l}_{s}}$
3. Calculate derivatives for every theta $\frac{\partial E}{\partial \theta_{ij}^{}}$
4. Add $\frac{\partial E}{\partial \theta}$ cumulatively to $\Delta$
   $\Delta^{(l)}_{i,j} := \Delta^{(l)}_{i,j} +$ $a_j^{(l)} \delta_i^{(l+1)}$ or in vectorial form $\Delta^{(l)} := \Delta^{(l)} + \delta^{(l+1)}(a^{(l)})^T$

END LOOP

$\frac{\partial E(\theta)}{\partial \theta }$ - final form of derivative after this training step

• Update $D^{(l)}_{i,j} := \dfrac{1}{m}\left(\Delta^{(l)}_{i,j} + \lambda\Theta^{(l)}_{i,j}\right)$ if j no equal 0 <- add derivative of regularization
• Update $D^{(l)}_{i,j} := \dfrac{1}{m}\Delta^{(l)}_{i,j}$ j = 0 <- no regularization for bias term

Elaboration about Derivatives

3. Step - Calculating $\frac{\partial E}{\partial z^{l}} = \delta^{l}$

Calculating $\frac{\partial E}{\partial z^{L}} = \delta^{L}$

It is important to note that $\delta$ is pretty much $\frac{\partial E}{\partial z}$ for all z.
Calculating $\delta^{L}$ is different from calculating $\delta^{L-1}$ $\delta^{L-2}$ … $\delta^{2}$

1. You have to calculate $\frac{\partial E}{\partial a^{L}} = \frac{y}{a^{L}}+\frac{(1-y)}{(1-a^{L})}$ and $\frac{\partial a}{\partial z^{L}}=(a^{L}* (1-a^{L}))=\sigma(z^{L})(1-\sigma(z^{L}))$

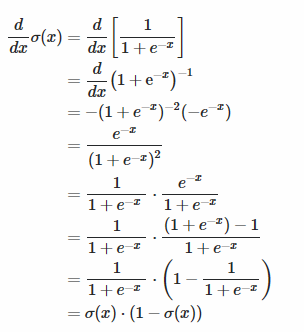
Here is the derivation for $\frac{\partial E}{\partial a}$

1. $$\frac{\partial E}{\partial z^{L}}=\frac{\partial E}{\partial a^{L}}* \frac{\partial a^{L}}{\partial z^{L}}= \delta^{(L)} = a^{L}* (1-a^{L})* (\frac{y}{a^{L}}+\frac{(1-y)}{(1-a^{L})})=a^{(L)} - y$$

Calculating $\frac{\partial E}{\partial z^{L-1}}=\delta^{(L-1)}, \frac{\partial E}{\partial z^{L-2}}=\delta^{(L-2)},\dots, \frac{\partial E}{\partial z^{2}}=\delta^{(2)}$ GENERAL CASE

Reminder: In each level l derivative we can have multiple $\delta^{l}$, like we have multiple $z^{l}$

Calculation is done somewhat recursively. For every smaller level $\delta^{l}$ we need to use $\delta^{l+1}$ in our calculation of the derivative because of the chain derivative rule: $\frac{d}\left[ {f\left( u(x) \right)} \right] = \frac{d}\left[ {f\left( u(x) \right)} \right]\frac$ . If, inside the formula we go further from the output in layer L towards the input in layer 1, we need to always take functions in between under consideration.

In other words

$\frac{\partial E}{z^{l}}=\frac{\partial E}{z^{l+1}}$ $\frac{\partial z^{l+1}}{ a^{l}} \frac{\partial a^{l}}{z^{l}}$ Here that part in bold stands for the part thats being added.

This translates to

$\frac{\partial E}{\partial Z^{l}} = \delta^{(l)} =$ $((\Theta^{(l)})^T \delta^{(l+1)})$ $\ .* \ a^{(l)}\ .* \ (1 - a^{(l)})$

Where each part stands for

• $((\Theta^{(l)})^T)=\frac{\partial z^{l+1}}{\partial a^{l}}$ $\theta^{l}a^{l}=z^{l+1}$ In $((\Theta^{(l)})^T)$ each row consists of derivatives for 1 single i-th $a^{l}_{i}$ for all $z^{l+1}$. For each $z^{l+1}$ we have multiple $a^{l}$ and column j in $((\Theta^{(l)})^T)$ consists of derivatives for $z^{l+1}_{j}$

• $((\Theta^{(l)})^T \delta^{(l+1)})=\frac{\partial E}{\partial a^{l}}$ in $\theta^{l}$ i-th row ańd j-th column we have $\frac{\partial z^{l+1}_{j}}{\partial a^{l}_{i}}$. The multiplication is going to have l num_layers X 1 dimensions.

  • This rule is somewhat more interesting, because it applies a somewhat complicated concept where 1 variable in a function affects the end result through multiple other functions. E.g $E=E(d(x),u(x))$ Such a function, when taking a derivative is solved by just summing up all the derivatives. This is somewhat intuitive but I wont go too deep into it
  • Explanation in Estonian of this rule

• $$\ a^{(l)}\ .* \ (1 - a^{(l)}) = \frac{\partial a^{l}}{z^{l}}$$

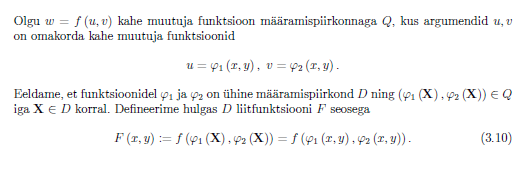
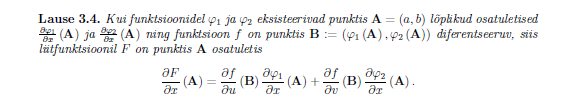
4. Step - Calculating $\frac{\partial E}{\partial \theta^{l}}$

Reminder

• $$z=\theta a$$
• 1 scalar $\theta$ has effect only on 1 z

$\frac{\partial E}{\partial \theta^{l}_{ij}}=\frac{\partial E}{z^{l+1}_{i}}$ $\frac{\partial z^{l+1}_{i}}{\partial \theta^{l}_{ij}}$

This in regular derivative form translates to

$$\frac{\partial E}{\partial \theta^{l}_{ij}}=\delta^{l+1}_{i}a^{l}_{j}$$

This translates in vectorial form to

$\delta^{(l+1)}(a^{(l)})^T$ results in i x j matrix, like $\theta$

Gradient Checking

https://www.coursera.org/learn/machine-learning/supplement/fqeMw/gradient-checking

• Do it for all the $\theta_{i}$-s and $\theta^{L}$ matrices

$$\dfrac{\partial}{\partial\Theta_j}J(\Theta) \approx \dfrac{J(\Theta_1, \dots, \Theta_j + \epsilon, \dots, \Theta_n) - J(\Theta_1, \dots , \Theta_j - \epsilon, \dots, \Theta_n)}{2\epsilon}$$

• For 1 matrix this looks like this.

thetaPlus=zeros(theta)
gradApprox=zeros(theta)
epsilon = 1e-4;
for i = 1:n,
  thetaPlus = theta;
  thetaPlus(i) += epsilon;
  thetaMinus = theta;
  thetaMinus(i) -= epsilon;
  gradApprox(i) = (J(thetaPlus) - J(thetaMinus))/(2*epsilon)
end;