LDA background - (messy - made for my own recap)

LDA ORIGIN,THEORY

• http://confusedlanguagetech.blogspot.com.ee/
• https://www.quora.com/What-is-a-good-explanation-of-Latent-Dirichlet-Allocation
• Helsinki University

Blei Article Summary

For every document in the collection, we generate the words in a two-stage process.

1. Randomly choose a distribution over topics.
2. For each word in the document
   • Randomly choose a topic from the distribution over topics in step #1.
   • Randomly choose a word from the corresponding distribution over the vocabulary.

For this we need

1. A space over distributions over topics.
2. A distribution over topics drawn from 1. (Also called the per-document distribution)
3. For each topic a distribution over vocabulary.

The central computational problem for topic modeling is to use the observed documents to infer the hidden topic structure. This can be thought of as “reversing” the generative process— what is the hidden structure that likely generated the observed collection?

LDA and probabilistic models. LDA and other topic models are part of the larger field of probabilistic modeling. In generative probabilistic modeling, we treat our data as arising from a generative process that includes hidden variables. This generative process defines a joint probability distribution [^joint_probability] over both the observed and hidden random variables.

We used observed variables (words in documtents) to get the distributions of hidden variables. The posterior distribution.7

LDA MORE FOMRALLY DESCRIBED

• Latent Random variable $\beta_{1:K}$ where each $\beta_{k}$ is a distribution over a fixed vocabulary
• Latent Random variable $\theta_{d}$ - topic proportions for document d where $\theta_{d,k}$ is a topic proportion for topic k for document d
• Latent Random variable $z_{d}$ where z_{d,n} is the topic assignement for n-th word in document d
• Observed Random variable $w_{d}$ where $w_{d,n}$ is the word assignement for n-th word in document d.

Alltogether with these random variables we can form the generative process defined join distribution.

$$\prod_{1:K} p(\beta_{k}) \prod_{1:D} p(\theta_{d}) \left(\prod_{1:N} p(z_{d,n} \vert \theta_{d})p(w_{d,n} \vert \beta_{1:K},d_{d,n})\right)$$

Posterior computation for LDA. We now turn to the computational problem, computing the conditional distribution of the topic structure given the observed documents. (As we mentioned, this is called the posterior.) Using our notation, the posterior

$p(\beta_{1:K}, \theta_{1:D}, z_{1:D} \vert w_{1:D})$=$\frac{p(\beta_{1:K}, \theta_{1:D}, z_{1:D}, w_{1:D})}{p(w_{1:D})}$

The numerator is the joint distribution of all the random variables, which can be easily computed for any setting of the hidden variables. The denominator is the marginal probability of the observations, which is the probability of seeing the observed corpus under any topic model. In theory, it can be computed by summing the joint distribution over every possible instantiation of the hidden topic structure. That number of possible topic structures, however, is exponentially large; this sum is intractable to compute.

NUMERATO - MURRU LUGEJA $\frac{a}{b}$ lugeja on a, b on nimetaja. Mixture Topic Model

• Formula
• PROBABALISTIC Model
• Observation Generation Description

Topic modeling algorithms form an approximation of Equation 2 by adapting an alternative distribution over the latent topic structure to be close to the true posterior. Topic modeling algorithms generally fall into two categories—sampling-based algorithms and variational algorithms. Sampling-based algorithms attempt to collect samples from the posterior to approximate it with an empirical distribution. The most commonly used sampling algorithm for topic modeling is Gibbs sampling, where we construct a Markov chain— a sequence of random variables, each dependent on the previous— whose maximal probability.) See Steyvers and Griffiths33 for a good description of Gibbs sampling for LDA, and see http:// CRAN.R-project.org/package=lda for a fast open-source implementation. Variational methods are a deterministic alternative to sampling-based algorithms.22,35 Rather than approximating the posterior with samples, variational methods posit a parameterized family of distributions over the hidden structure and then find the member of that family that is closest to the posterior.g Thus, the inference problem is transformed to an optimization problem. Variational methods open the door for innovations in optimization to have practical impact in probabilistic modeling.

What distributions are used.

DOCUMENT

It seems like the $theta$ and $beta$ are with dirichlet distirbution

TRAFFIC

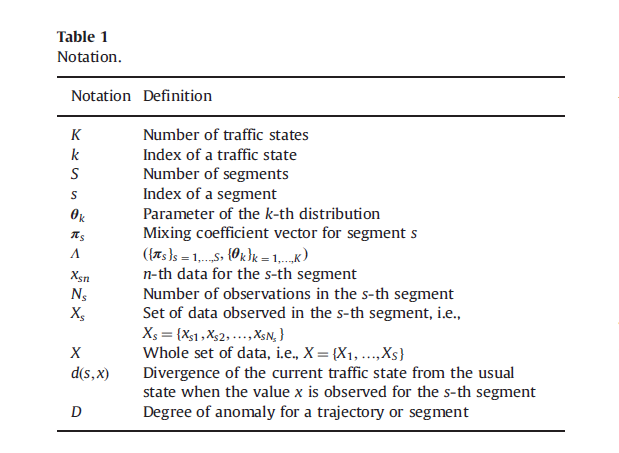
• $X_{s}$ - observations aggregated for segment s
• $x_{sn}$ - n-th observation of $X_{s}$ : segment s - In this paper we assume it is scalar (speed)
• This model associates every traffic state with a probability distribution.
  • We have K traffic states.
    • k-th traffic state corresponds to paremete $\theta_{k}$

• Every segment s is described as a mixture (a distribution) over these K traffic states. It is given by $p(x \vert s)= \sum_{k=1}^{K}{\pi_{sk} p(x \vert \theta_{k})}$ - IT IS A DISTRIBUTION

  • $0<=\pi <=1$ && $\sum_{k=1}^{K} \pi_{sk} = 1$
  • $\theta_{K}=(\theta_{1}...\theta_{K})$ State parameters are all same for all segments
  • $\pi_{s}=(\pi_{s1}...\pi_{sK})\intercal$ Segment parameters (multipliers for each traffic state) are different for all segments.

GENERATIVE PROCESS FOR THIS MODEL FOR EACH OBSERVATION ACCORDING TO THE PAPER :

• WORD BY WORD Choose a hidden state k~multinomial probability dis tribution $Multi(\pi_{s})$ This can be taken 2 ways

  • Choose a traffic state distribution for segment s. Choose a hidden state probability distribution k ~ multinomial distribution $Multi(\pi_{s})$. Kinda like choosing a topic distribution fir a document.
  • Choose a traffic state from a multinomial distribution $Multi(\theta_{s})$ Traffic state corresponds to topic. Topic assignement. It seems like the distribution among topics for each segment IS BINOMIAL.

• WORD BY WORD Generate the value $x_{sn}~p(x_{sn} \vert \theta_{k})$ This can be taken only 1 way

  • Draw an observation from state. This relates more to the 2 translation of the previous step: Choose a traffic state from a multinomial distribution $k~Multi(\pi_{s})$

SIMILIARITIES WITH DOCUMENT CLASSIFICATION

• Traffic state - Topic
• Segment - Document

PARAMETER ESTIMATION FOR HIDDEN STATES

We previously described a process for generation of each observation based on the Hidden random variables. Now we want to get those Hidden variables from each observation.

Lets first get likelihood function for X - L(X) For the entire set the likelihood of observed data is given by the following equation:

$$L(X)=\prod_{1}^{S} \prod_{1}^{N_{s}} \sum_{1}^{K}p(x_{sn} \vert \theta_{k})p(\pi_{sk})$$

It can be translated as: For each road segment for each observation the combined likelihood of drawing observations X

1. It seems like the distribution over topics for each segment IS BINOMIAL.
2. It seems like distribution over observations for each traffic state is Poisson

WHAT PARAMETERS ARE LEARNED

IN traffic states $\theta$ - state distribution over observations and $\pi$ segment distribution over states.

HOW THESE PARAMETES CAN BE LEARNED

EM ALGORITHM LEARNING PROCESS

• Why is the em algorithm used Väidetakse, et ta on optimaalsem kui likelihood maximization. Põhimõtteliselt asendab tavalisi likelihood approximatore.

• Likelihood of data - from this folder likelihood of data

• The log likelihood function

The joing density of n independent observation

$$f(y;\theta)=\prod_{i=1}^{n}f_{i}(y_{i};\theta)=L(\theta;y)$$

This expression viewed as a function of the unknown parameter $\theta$ given data y is called the likelihood. Often we work with the natural logarithm of the likelihood function, the so called- log likelihood function.

$$log L(\theta;y)=\sum_{i=1}^{n}log f_{i}(y_{i};\theta)$$

• EM ALGORITHM GREAT TUTORIAL
  • SOFT CLUSTERING - CLUSTERS MAY OVERLAP
  • EM ALGORITHM - MAXIMUM LIKELIHOOD ESTIAMTION PROBABALISTIC.
  • MIXTURE MODELS - PROBABILISTICALLY SOUND WAY TO DO SOFT CLUSTERING
• Q function - MIS ON SELLE SEOS EM ALGORITMING
• Bayesian inference in EM algorithm.Maximum likelihood and bayesian inference. Kui mõelda võimalikult lihtsalt siis maximum likelihood mõjutab bayesina inferenctsi.

LATENT VARIABLE LEARNING OVERALL

ESTIMATION VS INFERENCE 1 Answer

Estimation is but one aspect of inference where one substitutes unknown parameters (associated with the hypothetical model that generated the data) with optimal solutions based on the data (and possibly prior information about those parameters).

2 Answer

While estimation per se is aimed at coming up with values of the unknown parameters (e.g., coefficients in logistic regression, or in the separating hyperplane in support vector machines), statistical inference attempts to attach a measure of uncertainty and/or a probability statement to the values of parameters (standard errors and confidence intervals).

VARIATIONAL INFERENCE

Common methods for inferring latent variables

• Hidden Markov models
• Factor analysis
• Principal component analysis
• Partial least squares regression
• Latent semantic analysis and Probabilistic latent semantic analysis
• EM algorithms

Bayesian algorithms and methods

Bayesian statistics is often used for inferring latent variables.

• Latent Dirichlet Allocation
• The Chinese Restaurant Process is often used to provide a prior distribution over assignments of objects to latent categories.
• The Indian buffet process is often used to provide a prior distribution over assignments of latent binary features to objects.